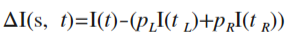決定木による学習
決定木は、根から順番に条件分岐を辿っていくことで結果を返します。特に分類問題で用いられる場合には「分類木」と呼ばれます。ここでは、与えられたデータを元に、自動的に分類木を構成する方法について説明します。機械学習の手法の中でも、学習結果を人間が解釈し易いことが特徴で、データの特徴を掴む場合によく用いられるようです。(「花びらの長さがθ以下ならチューリップ」などが分かれば、それだけで面白いですよね!)今回はアルゴリズムについて説明をした後、pythonでの実装例を紹介したいと思います。
CARTによる分類木の構築
CARTとはClassification And Regression Treesの略で、2進木の決定木の学習アルゴリズムです。決定木の学習アルゴリズムは他にもいくつか種類が有りますが、ここではCARTに絞って動作を見ていきたいと思います。
動作の流れ
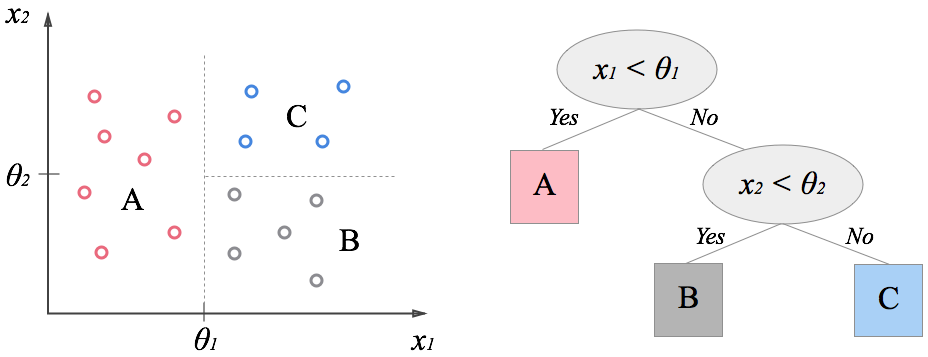
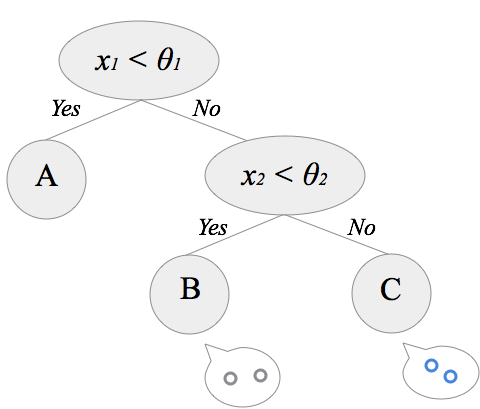
まず最初にルートノードに全データが与えられている状態を考えます。
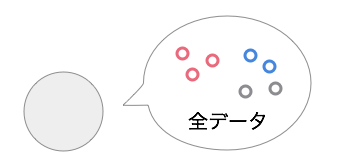
この全データを最も上手く分割する基準を探し(下で説明します)、データを2グループに分けます。自分の下に子ノードを2つ作成し、先ほど分割したデータをそれぞれ割り当てます。
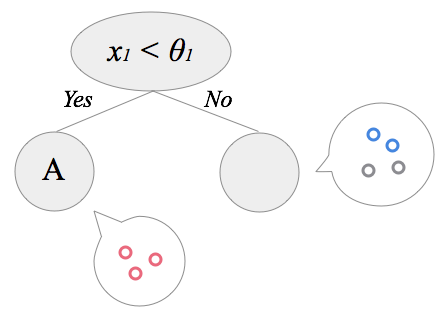
左の子ノードは1種類のデータのみになったのでここで終了です。右の子ノードはまだデータが混ざっているので、分割条件を探してデータを2つに分割します。あとはこの動作を繰り返し、再帰的に分割を続けていくと決定木が出来上がっていく、という流れです。
分割規則
ここではデータを2つに分割する方法について考えてみます。最初に、ノードに含まれるデータの「不純度」を定義し、分割による不純度の変化から、分割の良さを表す「分割指数」を定義します。最後に、分割の候補の選び方を紹介します。
(2) 分割の評価方法
次に、分割条件の善し悪しを判断するために、分割前後の不純度の変化を次式で定義します。(不純度にGini関数を用いる場合はGini Indexと呼ばれます。)
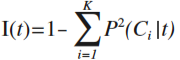
tはノードt、tLとtRは分割後の2つのグループを表します。pL、pRは分割後のノードの割合です。複数の分割条件sを試し、この分割指数が最大の分割を採用します。
(3) 分割候補の選び方
特徴量が数値の場合は次の考え方で候補を挙げることが出来ます。 「データをある特徴量に着目して小さい順に並べ、隣接する各ペアの中間地点を分割候補点とする。」 上の図では、特徴量はx1とx2です。まず、x1の小さい順でデータを並べ、隣り合うデータのx1の平均値が分割候補となります。x2についても同様に小さい順に並べ、各中間点を候補とします。これら全ての候補点で(2)の分割指数を計算し、最も分割指数の高い分割方法を採用します。
木の剪定
(1) 過学習の問題
まず質問。この分類をみてどう思いますか?
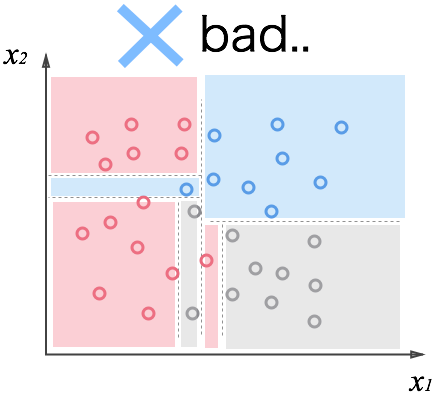
明らかにやり過ぎですね。与えられたデータはきちんと分けられていますが、過学習に陥ってしまっています。この状態に成らないために、「丁度良いところで止めたい」と思うのは自然だと思います。
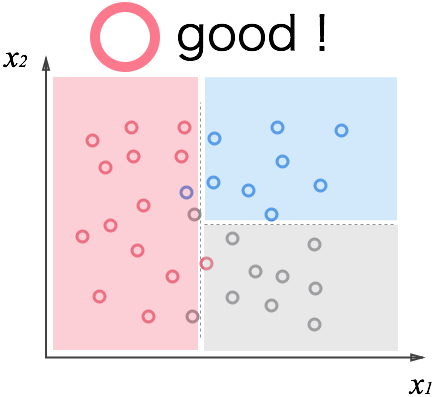
多少分類しきれないデータもありますが、この方がデータの特性をよく表していますよね。
(2) バランスの取り方
「学習度合い」と「木の複雑さ」のバランスを取るための方法は大きく分けると以下の2つ。
- a: 複雑になりすぎるまえに分岐処理を止める
- b: とりあえず分岐させておいて、後で不要な枝を剪定する
今回の実装編は(b)の方法でやっています。ここで問題になるのが「どの枝を剪定するか」という部分。以下のような基準で剪定する枝を選びます。
Fr = (分割指数) × (ノードに割り当てられたデータ数の割合)
分割指数が小さいのは、分割しても不純度があまり減らない「良くない分割」です。また、データ数の割合が小さいのは、細かい部分の分割を表しています。この2つの積であるFrに閾値を設けて、閾値に満たないノードは分割を取り消します。この評価を、先端のノードから順に行い、統合するかどうかを判断していきます。ちなみに、この閾値を調整することで、木の複雑さを制御できるようになります。
実装編
(1) 方針について
オブジェクト指向っぽく書きます。
まずは学習器本体の”DecisionTree”クラス。機能は以下の通り
- 生成時に調整パラメータを指定
- fit(data, target)で学習
- predict(data)で予測
- print_tree()でツリーの情報を吐き出し
次に木構造の単一ノードを表す”_Node”クラス。自ノードの配下に子ノードを保持することが出来ます。ファイル内部でしか使わないので、クラス名の頭にアンダースコアをつけてます。機能は以下の通り。
- build(data, target)で分類木の構築を行う
- 受け取ったデータを分割する規則を探し、子ノードを作って再帰的に呼び出します。
- prune(criterion, numall)で木の剪定を行う
- print_tree()でツリー情報を吐き出し
(2) コード
# -*- coding: utf-8 -*-
import numpy as np
class _Node:
"""決定木のノードクラス"""
def __init__(self):
"""初期化処理
left : 左の子ノード(しきい値未満)
right : 右の子ノード(しきい値以上)
feature : 分割する特徴番号
threshold : 分割するしきい値
label : 割り当てられたクラス番号
numdata : 割り当てられたデータ数
gini_index : 分割指数(Giniインデックス)
"""
self.left = None
self.right = None
self.feature = None
self.threshold = None
self.label = None
self.numdata = None
self.gini_index = None
def build(self, data, target):
"""木の構築を行う
data : ノードに与えられたデータ
target : データの分類クラス
"""
self.numdata = data.shape[0]
num_features = data.shape[1]
# 全データが同一クラスとなったら分割終了
if len(np.unique(target)) == 1:
self.label = target[0]
return
# 自分のクラスを設定(各データの多数決)
class_cnt = {i: len(target[target==i]) for i in np.unique(target)}
self.label= max(class_cnt.items(), key=lambda x:x[1])[0]
# 最良の分割を記憶する変数
best_gini_index = 0.0 # 不純度変化なし
best_feature = None
best_threshold = None
# 自分の不純度は先に計算しておく
gini = self.gini_func(target)
for f in range(num_features):
# 分割候補の計算
data_f = np.unique(data[:, f]) # f番目の特徴量(重複排除)
points = (data_f[:-1] + data_f[1:]) / 2.0 # 中間の値を計算
# 各分割を試す
for threshold in points:
# しきい値で2グループに分割
target_l = target[data[:, f] < threshold]
target_r = target[data[:, f] >= threshold]
# 分割後の不純度からGiniインデックスを計算
gini_l = self.gini_func(target_l)
gini_r = self.gini_func(target_r)
pl = float(target_l.shape[0]) / self.numdata
pr = float(target_r.shape[0]) / self.numdata
gini_index = gini - (pl * gini_l + pr * gini_r)
# より良い分割であれば記憶しておく
if gini_index > best_gini_index:
best_gini_index = gini_index
best_feature = f
best_threshold = threshold
# 不純度が減らなければ終了
if best_gini_index == 0:
return
# 最良の分割を保持する
self.feature = best_feature
self.gini_index = best_gini_index
self.threshold = best_threshold
# 左右の子を作って再帰的に分割させる
data_l = data[data[:, self.feature] < self.threshold]
target_l = target[data[:, self.feature] < self.threshold]
self.left = _Node()
self.left.build(data_l, target_l)
data_r = data[data[:, self.feature] >= self.threshold]
target_r = target[data[:, self.feature] >= self.threshold]
self.right = _Node()
self.right.build(data_r, target_r)
def gini_func(self, target):
"""Gini関数の計算
target : 各データの分類クラス
"""
classes = np.unique(target)
numdata = target.shape[0]
# Gini関数本体
gini = 1.0
for c in classes:
gini -= (len(target[target == c]) / numdata) ** 2.0
return gini
def prune(self, criterion, numall):
"""木の剪定を行う
criterion : 剪定条件(この数以下は剪定対象)
numall : 全ノード数
"""
#自分が葉ノードであれば終了
if self.feature == None:
return
# 子ノードの剪定
self.left.prune(criterion, numall)
self.right.prune(criterion, numall)
# 子ノードが両方葉であれば剪定チェック
if self.left.feature == None and self.right.feature == None:
# 分割の貢献度:GiniIndex * (データ数の割合)
result = self.gini_index * float(self.numdata) / numall
# 貢献度が条件に満たなければ剪定する
if result < criterion:
self.feature = None
self.left = None
self.right = None
def predict(self, d):
"""入力データ(単一)の分類先クラスを返す"""
# 自分が節の場合は条件判定
if self.feature != None:
if d[self.feature] < self.threshold:
return self.left.predict(d)
else:
return self.right.predict(d)
# 自分が葉の場合は自分の分類クラスを返す
else:
return self.label
def print_tree(self, depth, TF):
"""分類条件を出力する"""
head = " " * depth + TF + " -> "
# 節の場合
if self.feature != None:
print head + str(self.feature) + " < " + str(self.threshold) + "?"
self.left.print_tree(depth + 1, "T")
self.right.print_tree(depth + 1, "F")
# 葉の場合
else:
print head + "{" + str(self.label) + ": " + str(self.numdata) + "}"
class DecisionTree:
"""CARTによる分類木学習器"""
def __init__(self, criterion=0.1):
"""初期化処理
root : 決定木のルートノード
criterion : 剪定の条件
(a) criterion(大) -> 木が浅くなる
(b) criterion(小) -> 木が深くなる
"""
self.root = None
self.criterion = criterion
def fit(self, data, target):
"""学習を行い決定木を構築する
data : 学習データ
target : 各データの分類クラス
"""
self.root = _Node()
self.root.build(data, target)
self.root.prune(self.criterion, self.root.numdata)
pass
def predict(self, data):
"""分類クラスの予測を行う
data : テストデータ
"""
ans = []
for d in data:
ans.append(self.root.predict(d))
return np.array(ans)
def print_tree(self):
"""分類木の情報を表示する"""
self.root.print_tree(0, " ")