巡回セールスマン問題
巡回セールスマン問題(Traveling Salesman Problem; TSP)は都市の集合と各2都市間の移動コスト(例えば距離)が与えられた時に、全ての都市を1回ずつ訪問して出発地にもどる経路の総移動コストを最小化する最適化問題です。組み合わせ最適化問題の代表例としてよく説明に使われます。今回は、代表的なアルゴリズムをPythonで実装して、動作を見ていきたいと思います。
%matplotlib inline import numpy as np import matplotlib.pyplot as plt plt.style.use('ggplot')
経路のパターン数
まず、この問題は全パターンをごり押しで計算できるか考えてみます。機械的に全通りの経路を調べて、最適解を見つけられるならそれが一番です。都市数をNとして、何パターンの経路があるのかを計算してみます。
ある経路を選んだ時に、どこから出発するかでN通りの回り方がありますが、経路が同じであれば総移動コストは同じです。なので、重複して計算するのを避けるために、出発地は固定して考えます。出発地を決めると、最初に向かう都市の選択肢は(N-1)個、次の移動では(N-2)個、さらにその次の移動では(N-3)個、のようになります。つまり、(N-1)×(N-2)×(N-3)×...×1 = (N-1)! 通りの経路があります。
都市数を1〜20に変えて具体的な値を計算してみます。
import math for n in range(1, 21): print('N = {}: (N-1)! = {}'.format(n, math.factorial(n - 1)))
N = 1: (N-1)! = 1 N = 2: (N-1)! = 1 N = 3: (N-1)! = 2 N = 4: (N-1)! = 6 N = 5: (N-1)! = 24 N = 6: (N-1)! = 120 N = 7: (N-1)! = 720 N = 8: (N-1)! = 5040 N = 9: (N-1)! = 40320 N = 10: (N-1)! = 362880 N = 11: (N-1)! = 3628800 N = 12: (N-1)! = 39916800 N = 13: (N-1)! = 479001600 N = 14: (N-1)! = 6227020800 N = 15: (N-1)! = 87178291200 N = 16: (N-1)! = 1307674368000 N = 17: (N-1)! = 20922789888000 N = 18: (N-1)! = 355687428096000 N = 19: (N-1)! = 6402373705728000 N = 20: (N-1)! = 121645100408832000
N = 10を超えた辺りからえげつないことになっていますね。都市数が20とかのレベルになると、全通り試すのは明らかにしんどいです。ということで、総当たりでの厳密解法は難しそうですので、近似解法を試していくことにします。(わざとらしい...。)
問題設定
まず最初に、この記事で扱う問題を定義しておきたいと思います。
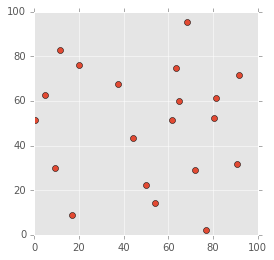
- 都市数を20にして、各都市の位置をランダムに設定
- 各都市間の移動コストは距離とする
ということで、まずは都市の位置を準備します。
N = 20 MAP_SIZE = 100 np.random.seed(10) city_xy = np.random.rand(N, 2) * MAP_SIZE plt.figure(figsize=(4, 4)) plt.plot(city_xy[:, 0], city_xy[:, 1], 'o') plt.show()
総移動距離の計算
次に、総移動距離の計算をする関数を用意します。これが訪問順の評価指標となります。距離を何度も計算するのはもったいないので、先に都市間の距離を計算しておきます。
x = city_xy[:, 0] y = city_xy[:, 1] distance_matrix = np.sqrt((x[:, np.newaxis] - x[np.newaxis, :]) ** 2 + (y[:, np.newaxis] - y[np.newaxis, :]) ** 2) # 見やすくするために10都市分だけ出力。 # distance_matrix[i, j]が都市iと都市jの距離。 print(np.round(distance_matrix[:10, :10]))
[[ 0. 74. 34. 94. 61. 94. 91. 59. 28. 71.] [ 74. 0. 54. 44. 81. 21. 67. 22. 47. 29.] [ 34. 54. 0. 61. 36. 75. 57. 50. 23. 64.] [ 94. 44. 61. 0. 67. 52. 32. 63. 70. 72.] [ 61. 81. 36. 67. 0. 101. 45. 83. 59. 98.] [ 94. 21. 75. 52. 101. 0. 81. 36. 66. 33.] [ 91. 67. 57. 32. 45. 81. 0. 81. 75. 94.] [ 59. 22. 50. 63. 83. 36. 81. 0. 33. 15.] [ 28. 47. 23. 70. 59. 66. 75. 33. 0. 47.] [ 71. 29. 64. 72. 98. 33. 94. 15. 47. 0.]]
def calculate_total_distance(order, distance_matrix): """Calculate total distance traveled for given visit order""" idx_from = np.array(order) idx_to = np.array(order[1:] + [order[0]]) distance_arr = distance_matrix[idx_from, idx_to] return np.sum(distance_arr)
# 試しに距離を計算してみる test_order = list(np.random.permutation(N)) print('訪問順序 = {}'.format(test_order)) total = calculate_total_distance(test_order, distance_matrix) print('総移動距離 = {}'.format(total))
訪問順序 = [9, 14, 0, 12, 15, 6, 1, 11, 16, 2, 3, 7, 4, 18, 19, 5, 17, 10, 13, 8] 総移動距離 = 1079.4019034407843
訪問経路の可視化
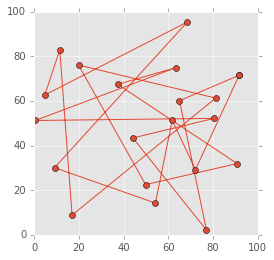
経路を可視化するコードも先に準備しておきます。こういう計算をする時に、数字だけ見て作業をするよりも色々気付きがあるので、可視化大事です。あと、「やってる感」が出てやる気が出ます。(笑)
def visualize_visit_order(order, city_xy): """Visualize traveling path for given visit order""" route = np.array(order + [order[0]]) # add point of departure x_arr = city_xy[:, 0][route] y_arr = city_xy[:, 1][route] plt.figure(figsize=(4, 4)) plt.plot(x_arr, y_arr, 'o-') plt.show()
# 可視化を試してみる visualize_visit_order(test_order, city_xy)
局所探索法
組み合わせ最適化でよく使われる、局所探索法を使ってよい訪問経路を探してみます。この方法は、現在の解に少し変化を加え、目的とする指標値(ここでは総移動距離)が改善されたら、その解を採用します。この操作を繰り返し、これ以上改善が見られなくなった時点で終了します。
2-opt近傍
この「現在の解に少し変化を加える」方法は問題毎にさまざまな方法が提案されています。ここでは、循環セールスマン問題でよく使われる近傍の例として、2-opt近傍を使います。2-opt近傍は、経路中の2本の移動を交換するものです。素直に実装すると、交換前後でそれぞれ総移動距離を計算して比較すれば良いのですが、結局交換した部分のみ考えても同じことなので、交換による総移動距離の差分を計算する関数を準備します。
def calculate_2opt_exchange_cost(visit_order, i, j, distance_matrix): """Calculate the difference of cost by applying given 2-opt exchange""" n_cities = len(visit_order) a, b = visit_order[i], visit_order[(i + 1) % n_cities] c, d = visit_order[j], visit_order[(j + 1) % n_cities] cost_before = distance_matrix[a, b] + distance_matrix[c, d] cost_after = distance_matrix[a, c] + distance_matrix[b, d] return cost_after - cost_before
以下が、2つのパスの交換後の訪問順序を計算するコードになります。
def apply_2opt_exchange(visit_order, i, j): """Apply 2-opt exhanging on visit order""" tmp = visit_order[i + 1: j + 1] tmp.reverse() visit_order[i + 1: j + 1] = tmp return visit_order
近傍探索の実装
現状の訪問経路の、各2パスを入れ替える操作を全組み合わせで実施します。全通りを計算しておき、もっとも総移動距離を減らせる交換を実際に適用します。これ以上改善できなければNoneを返すことにします。
def improve_with_2opt(visit_order, distance_matrix): """Check all 2-opt neighbors and improve the visit order""" n_cities = len(visit_order) cost_diff_best = 0.0 i_best, j_best = None, None for i in range(0, n_cities - 2): for j in range(i + 2, n_cities): if i == 0 and j == n_cities - 1: continue cost_diff = calculate_2opt_exchange_cost( visit_order, i, j, distance_matrix) if cost_diff < cost_diff_best: cost_diff_best = cost_diff i_best, j_best = i, j if cost_diff_best < 0.0: visit_order_new = apply_2opt_exchange(visit_order, i_best, j_best) return visit_order_new else: return None
上で実装した2-optによる近傍探索を、改善が見られる限り繰り返します。
def local_search(visit_order, distance_matrix, improve_func): """Main procedure of local search""" cost_total = calculate_total_distance(visit_order, distance_matrix) while True: improved = improve_func(visit_order, distance_matrix) if not improved: break visit_order = improved return visit_order
これで近傍探索のコードは完成です。早速、近傍探索を動かしてみましょう。
# 適当に初期解を生成 test_order = list(np.random.permutation(N)) visualize_visit_order(test_order, city_xy) total_distance = calculate_total_distance(test_order, distance_matrix) print('初期解の総移動距離 = {}'.format(total_distance)) # 近傍を計算 improved = local_search(test_order, distance_matrix, improve_with_2opt) visualize_visit_order(improved, city_xy) total_distance = calculate_total_distance(improved, distance_matrix) print('近傍探索適用後の総移動距離 = {}'.format(total_distance))
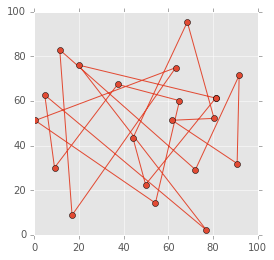
初期解の総移動距離 = 1089.0058941597254
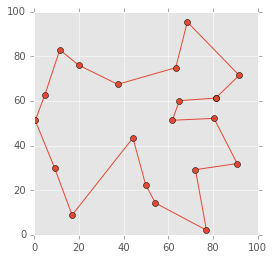
近傍探索適用後の総移動距離 = 420.08788455293126
ランダムの初期解に従って各都市を回ってこい!と言われたら心が折れそうですよね。それに対して近傍探索で改善を行った経路の方は、近い都市を順番にまわるような経路に改善されているのが分かります。
多スタート戦略
近傍探索の簡単な拡張として、多スタート戦略を試してみたいと思います。近傍探索は与えられた解から改善を繰り返していきますが、最終的に得られる解の良さは、初期解によって変わります。偶然いい感じの解からスタートできれば良い解が得られますが、いまいちの解を改善していっても良い解は得られません。そこで、ランダムに初期解を生成して近傍探索をする、というのを複数セット実施することで、より安定して良い解が得られるようになります。
以下では、ランダムな初期値からの近傍探索を100回繰り返すコードを書いてみました。
import sys N_START = 100 order_best = None score_best = sys.float_info.max for _ in range(N_START): order_random = list(np.random.permutation(N)) order_improved = local_search( order_random, distance_matrix, improve_with_2opt) score = calculate_total_distance(order_improved, distance_matrix) if score < score_best: score_best = score order_best = order_improved visualize_visit_order(order_best, city_xy) total_distance = calculate_total_distance(order_best, distance_matrix) print('多スタート戦略で得られた経路の総移動距離 = {}'.format(total_distance))
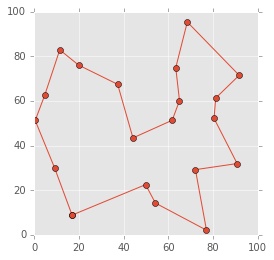
多スタート戦略で得られた経路の総移動距離 = 396.17695563609686
いい感じですね。最初に経路のパターン数を見たときはお、おう、、となりましたが、今回の方法で良い解を現実的な計算時間で得ることができました。(100回の多スタート戦略でも、手元の環境では1秒程度で計算が終わります。)
まとめ
- 都市数20程度と、それほど問題規模が大きくなくても、組み合わせパターンは膨大になります。厳密解が計算できないので、近似解法を考えます。
- 組み合わせ最適問題の近似解法としてよく使われる「近傍探索法」による解の改善アルゴリズムを実装しました。単純な仕組みですが、かなり良い経路を見つけることができました。
- さらに、多スタート戦略を取り入れることで、安定してよい解が得られることを確認しました。
まずは代表的なテーマを、と思い巡回セールスマン問題を動かしてみました。Deep Learningばかりに注目が集まっている今日この頃ですが、こういった手法を効果的に取り入れていきたいなあと思ってます。
最後までお付き合いいただきありがとうございました。それではまた。
